i = i++

This expression, and many like it, demonstrate the sequencing rules of C++ and how they can cause your program to behave in ways you might not expect. What should the result of this expression be given some initial value for i? Questions like this are extremely frequent on Stack Overflow. In this case, the answer is that this code is completely undefined — it could do anything. Literally anything (at least formally speaking).

The C++ standard defines an execution path according to your code. Given particular inputs, the program will always follow this execution path. Sometimes, the standard allows multiple possible execution paths for your program. This gives compilers extra freedom to optimize in various ways. When the standard allows a particular set of possible paths, this is known as unspecified behavior. In other cases, the standard gives absolutely no requirements about the behavior of your program, and this is known as undefined behavior. Undefined behavior is certainly not something you want in your code.

The sequencing rules of C++, which describe how the evaluations of expressions and their subexpressions are ordered, may determine that an expression is undefined. C++11 introduced a smarter but slightly more complex approach to specifying these rules, which is still used in C++14. There’s a great overview of the rules on the cppreference.com wiki.

In simple terms, evaluations are ordered by a sequenced-before relationship. That is, evaluation of one part of an expression may be sequenced-before the evaluation of another part. Evaluations can be one of two things: value computations, which work out the result of an expression; and side effects, which are modifications of objects. When two evaluations are not sequenced-before each other, they are unsequenced (we cannot say which will occur first and they may even overlap).

Informally, the basic sequencing rules are as follows:

• The value computation of an operator’s operands are sequenced before the value computation of its result — else how would we compute the result? Note, however, that the side effects of the operands are not necessarily sequenced-before.
• In general, the evaluation of an operator's operands are unsequenced with respect to each other. For example, in x + y, the evaluation of x and y are unsequenced.
• For &&, ||, and ,, however, evaluation of the left operand is sequenced before the right operand.
• The value computation of postfix ++ and -- is sequenced before their side effects.
• The side effects of prefix ++ and -- are sequenced before their value computation.
• The value computations of the operands of any assignment operator (=, +=, -=, etc.) are sequenced before the side effect of the assignment, which is itself sequenced before value computation of the assignment expression.

The rules that define when the sequenced-before relationship exists between two evaluations inherently form an acyclic directed graph structure. As an example, let’s consider the earlier line of code once again:

i = i++

Let's first split it up into its subexpressions. The full expression is the assignment, which has two operands. The left operand is just i, while the right operand is i++ which itself has i as an operand. The following tree represents this structure, where the arrows represent the sequenced-before relationship of the value computations of those subexpressions:

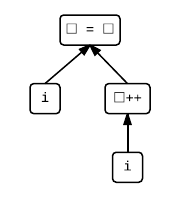
Both the assignment and the increment have side effects (i.e. they modify the value of an object). We know how they are sequenced with respect to the value computations by looking at the above sequencing rules. The assignment comes after the value computation of its operands and before its own value computation. The increment comes after its value computation, but is not sequenced-before the assignment. If we add them as red nodes, we have:

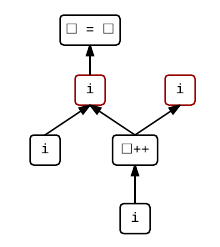
We can read this graph as flowing chronologically upwards. For the purposes of determining undefined behavior, we also need to identify any value computations that use the value of an object. This is quite a subtle point, but only value computations of expressions denoting objects (like i) that are being used where an rvalue is expected are value computations that use the value of an object. When such an expression is used where an lvalue is expected instead, its value is not important, as in the left operand of =.

If we highlight value computations that use the value of objects in blue, we get:

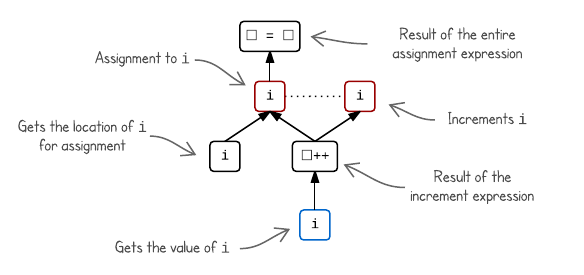
Notice the interesting placement of the i increment — nothing else is sequenced after it, so it could even occur after the assignment. Herein lies the undefined behaviour. Depending on whether the increment occurs before or after the assignment, we could get different results.

To determine whether an expression might be undefined, we can simply look at its graph. Two evaluations in different branches are completely unsequenced (that is, if there is no directed path between them). The standard states that we have undefined behaviour if: we have two side effects on the same scalar object that are unsequenced; or we have a side effect on a scalar object and a value computation using the value of the same object that are unsequenced. In the above graph, I have connected the problematic pair of evaluations with a dotted line — two unsequenced side effects.

As you can see, this gives a great way to visualize the sequencing rules as applied to a particular expression and makes it much easier to see why certain expressions might result in undefined behaviour.

Let’s take a look at some more examples of both undefined and well-defined expressions:

i = ++i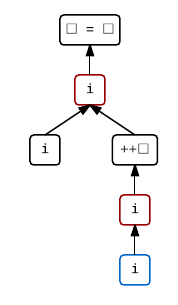

It is interesting to see that by merely switching the postfix increment to a prefix increment, this expression has become well-defined. That’s because the increment of i has to occur before the value computation of the increment expression and, therefore, before the assignment to i.

i = i++ + i++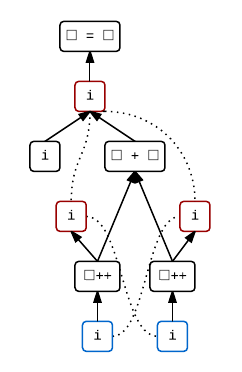

This is a slightly more complex adaptation of the expression we first looked at. It seems to be quite a popular example. It has undefined behaviour for the same reasons, but also exhibits unsequenced side effects and value computations between the two increments. In the same way, i++ + i++ alone is undefined.

i = v[i++]

This one tends to be hard for many to grasp, although its problem is exactly the same as the previous examples. I suspect that most people think of i++ as an operation that “returns the value of i, then increments i.” The problem is that the increment can happen at any point, and might happen after the assignment to i. The fact that we're using it as a subscript doesn't change anything.

i++ || i++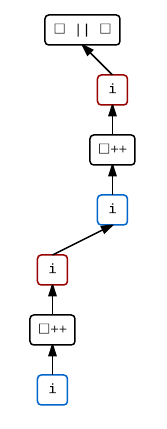

This demonstrates the ability of some operators (namely ||, &&, and ,) to enforce sequencing between their operands. The standard states that every value computation and side effect associated with the left operand is sequenced before those of the right operand.

f(i = 1, i = 2)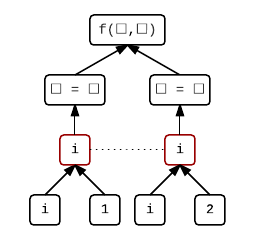

Here we’re calling a function and in each argument we’re assigning a different value to i. The evaluations of function arguments are also unsequenced, so we cannot say what the value of i will be after this expression has been evaluated.

It’s worth noting that function calls are always indeterminately sequenced. This means that one always occurs before the other, but we cannot say which way around. This is to prevent function calls from interleaving. However, the undefined behaviour rule only applies with unsequenced evaluations. Therefore, if you have two function calls in different branches that modify the same scalar object, you don’t have undefined behaviour — instead you have unspecified behaviour.

Also remember that overloaded operators are actually treated as function calls. That is, if you want to know how x + y is sequenced, and operator+ is overloaded for x, you need to treat the expression as x.operator+(y) or operator+(x, y) — whichever is defined.

Finally, it is not always enough to look at the identifiers in expressions. Previously, we noted that an object i was modified in two parts of an expression. However, it’s possible to have two different identifiers, say i and j, that either refer to the same scalar object or are more complex data types that have a shared scalar object that they modify. Keep this in mind.

Next time you come across a complex expression (which is hopefully not very often), you now have a great way to analyse the sequencing of evaluations and determine the possible execution paths of that expression. Perhaps this might reduce the number of questions on Stack Overflow about this topic, but if not, at least it gives a nice visual way to answer them.